在大数据时代，数据分析无疑是最红火的技术之一。随着我国医疗卫生事业的发展与壮大，广大医学工作者对数据分析方法的需求也越来越大。医学数据分析已经成为当前的热门领域，它是医学、统计学和计算机科学等领域的交叉学科。数据分析离不开软件。R是一款免费开源软件，它提供了先进的统计计算与可视化功能。

R语言的前身是S语言，S语言是和他的同事们于1976年在贝尔实验室开发的一种专用于统计分析的解释型语言。这种语言后来发展成一个商用版本S-PLUS，并被全世界的统计学家广泛使用。

1992年，新西兰奥克兰大学的RossIhaka和RobertGentleman为了教学目的基于S语言开发了一门新的语言，并根据二人名字的首字母，将其命名为R。1995年，R作为开源软件发布，两位作者也吸纳了其他开发者参与R的更新。到了1997年的时候，成立了11人的R语言核心团队，从2011年至今，该团队一直维持在20人。

R语言早期主要是学术界统计学家在用，后来逐渐被其他很多领域的学者使用。尤其是随着大数据的爆发，越来越多有计算机和工程背景的人加入这个圈子，对R的计算引擎、性能以及各种程序包进行改进和升级，大大推动了R语言的发展。

为什么使用R分析数据

医学数据分析是统计学与医学专业知识的结合。而无论是统计计算还是数据的可视化都离不开计算机软件。市面上有很多流行的统计和作图软件，如SAS、SPSS、Stata等。为何要选择R呢？具体来讲，R有如下优势。

（1）大多数统计软件需要付费，而R是基于GNU通用公共许可协议发布的，它可以免费使用和传播。

（2）R可以在多种平台下使用，如Windows、macOS、各种版本的Linux和UNIX等。有用户甚至在浏览器和手机操作系统上运行R。

（3）R编程简单，仅需要熟悉一些函数的参数和用法，不需要了解程序实现的细节。

（4）R小巧但功能强大，被称为数据分析界的“瑞士军刀”。R的安装文件大小不到100MB，大部分函数存在于扩展包里。这些扩展包涵盖了各行各业中数据分析的前沿方法。

（5）R实现了可重复性分析，用户可以从重复性分析工作中抽身出来，也能与同行分享分析过程并从中获益。借助R及其扩展包，用户能在一份文档中混合编写R代码和标记文本，并自动生成分析报告。

但是R也存在一些固有缺点，例如学习曲线相对比较陡峭、第三方包的质量良莠不齐等。在本书的学习过程中，建议读者“边学边做”，即输入书中的代码、观察输出结果，并尝试改变代码（例如函数里的参数）以掌握R的用法。另外，建议读者尽量使用官方网站的扩展包或者有经验的用户推荐的包。

书籍推荐：

R语言医学数据分析实战

本着让非统计专业读者易理解的原则，本书强调实战和应用，着重介绍数据分析的思路和方法，以及数据分析的实质、特点、应用条件和结果，尽量淡化统计方法的推导和计算。第1章和第2章介绍了R语言的基本用法；第3章介绍了数据预处理的方法，涵盖了基本的数据处理和一些高级数据操作的技巧；第4章介绍了如何用R语言进行数据可视化；第5章介绍了基本统计分析方法，包括描述性统计分析和各种单因素分析方法；第6章至第8章结合实际数据介绍了医学研究中最常用的三种回归模型，即线性回归、Logistic回归和Poisson回归；第9章介绍了生存分析；第10章至第12章介绍了几种最常用的多元分析方法，即聚类分析、判别分析、主成分分析和因子分析；第13章介绍了临床诊断试验的评价指标和计算方法；第14章介绍了循证医学研究中常用的Meta分析方法。

本书适合临床医学、公共卫生及其他医学相关专业的本科生或研究生使用，亦可作为其他专业的学生和科研工作者进行数据分析的参考书。读者可以从头至尾逐章学习，也可以根据自己在实际中遇到的问题有选择地在相应章节寻找解决方案。希望本书能够让读者更深入地理解数据分析，并进一步促进R语言在国内的普及。

目录

第1章R语言介绍

第2章创建数据集

第3章数据框的操作

第4章数据可视化

第5章基本统计分析

第6章线性回归分析

第7章Logistic回归分析

第8章Poisson回归分析

第9章生存分析

第10章聚类分析

第11章判别分析

第12章主成分分析和因子分析

第13章临床诊断试验评价

第14章Meta分析

样章截选：第6章线性回归分析

在医学科研与实践中，经常需要探索一个结果变量与其他变量之间的关系，如糖尿病的血糖变化可能受胰岛素、血清总胆固醇、甘油三酯等多种生化指标的影响。本章介绍的线性回归模型包含一个连续型的结果变量（或称因变量）和一个或多个解释变量（或称自变量）。当解释变量只有一个时，模型称为简单线性回归（simplelinearregression）或直线回归；当解释变量多于一个时，模型称为多重线性回归（multiplelinearregression）。

6.1简单线性回归

简单线性回归模型假定因变量Y只受一个自变量X影响，它们之间存在着近似的线性函数关系，模型可表示为

其中，因变量Y被分解为两部分：一部分是由X的变化所确定的Y线性变化的部分，用X的线性函数α+βX表示，其中α被称为常数项（截距项），β被称为回归系数（斜率项）；另一部分是其他随机因素的影响部分，被看作随机误差，用ε表示，并假设ε服从均值为0、方差为σ2的正态分布。

load("")library(epiDisplay)des(UCR)=18VariableClassDescription1ageintegerAgeinyears2ucrnumericUrinecreatinine(mmol)3groupfactorTypeofchildrensummary(UCR)ageucrgroupMin.:6.00Min.:2.2100:81stQu.:8.251stQu.:2.6721:10Median:10.00Median:3.010Mean:10.50Mean:3.0163rdQu.:12.003rdQu.:3.315Max.:16.00Max.:3.980

数据框UCR包含3个变量和18条记录。数据中没有缺失值，可以直接用于分析。

6.1.1拟合简单线性回归模型

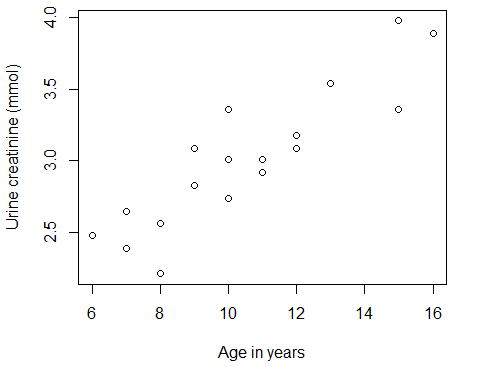
对于所有的数据分析来说，第一步总是探索数据。散点图是判断变量间是否存在线性关系的、非常有用的工具。我们先借助散点图探索年龄和尿肌酐含量之间的关系。

plot(ucr~age,data=UCR,+xlab="Ageinyears",ylab="Urinecreatinine(mmol)")

从图6-1可以看出，尿肌酐含量随着年龄的增加而增加且呈直线趋势。

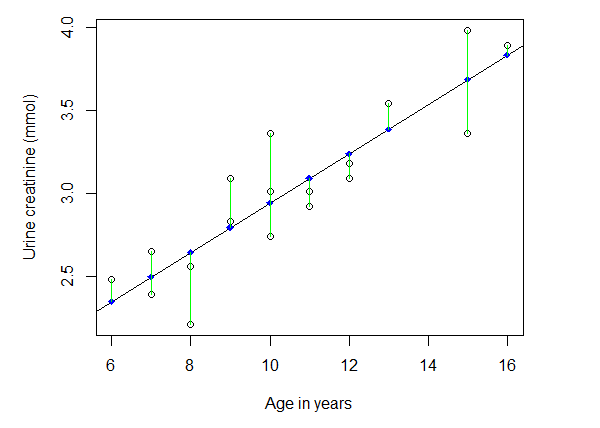
图6-1年龄与尿肌酐含量散点图

为了拟合回归直线，下面用函数lm()建立线性回归模型。

mod-lm(ucr~age,data=UCR)modCall:lm(formula=ucr~age,data=UCR)Coefficients:(Intercept)

直接输出建立的模型对象mod只会显示关于模型的非常有限的信息。为了获得更多关于该模型的信息，我们可以用函数attributes()查看该模型对象的属性。

attributes(mod)$names[1]"coefficients""residuals""effects""rank"""[6]"assign""qr""""xlevels""call"[11]"terms""model"$class[1]"lm"

对象mod一共包含12个属性，我们可以单独提取某个属性。例如，下面的命令可以得到模型的拟合值。

mod$

6.1.2模型输出结果的解释

使用函数summary()可以汇总显示模型的大部分属性。

summary(mod)Call:lm(formula=ucr~age,data=UCR)Residuals::(|t|)(Intercept)1.454920.207127.0252.87e-06******---:0‘***’0.001‘**’0.01‘*’0.05‘.’0.1‘’1Residualstandarderror:0.2289on16degreesoffreedomMultipleR-squared:0.7921,AdjustedR-squared:0.7791F-statistic:60.95on1and16DF,p-value:7.597e-07

上面输出的第一个部分显示了模型调用的公式。第二个部分给出了残差的分布，残差的中位数接近于0，最大值（0.41823）与最小值（−0.43440）的绝对值很接近，下四分位数（−0.13828）与上四分位数（0.14738）的绝对值也很接近。这表明残差的分布基本上是对称的。第三个部分给出了模型的回归系数的估计值，包含常数项（截距）和年龄对尿肌酐含量影响的系数（斜率）。其中，常数项1.45492表示年龄为0时的尿肌酐含量，这显然没有实际意义。其对应的p值为2.87×10−6，仅表示该常数项与0之间的差异非常显著。变量age的系数为0.14869，表示年龄每增长一岁，尿肌酐含量平均增加0.14869mmol。虽然0.14869的数值很小，但它与0有高度显著的差异（p值为7.60×10−7）。

决定系数（R2）的值为0.7921，表示数据中有79.2%的变异能被该模型解释；调整后的决定系数的值为0.7791。我们将在下面对模型的方差分析中给出二者的计算方法。最后一个部分对残差做了更详细的描述，并采用F统计量对变量age的效应做了假设检验。该检验的p值（7.597×10−7）与上面对回归系数的t检验的p值相等。F检验更经常出现在模型的方差分析表中。

summary(aov(mod))DfSumSqMeanSqFvaluePr(F)***:0‘***’0.001‘**’0.01‘*’0.05‘.’0.1‘’1

SST-sum((UCR$ucr-mean(UCR$ucr))^2);SST[1]4.033028

残差平方和为：

SSR-sum(residuals(mod)^2);SSR[1]0.8385279

回归平方和，即拟合值与总均值之差的平方和为：

SSW-sum((fitted(mod)-mean(UCR$ucr))^2);SSW[1]3.1945

后两个平方和相加等于总的平方和。决定系数就是回归平方和与总的平方和的比值。

SSW/SST[1]0.7920848

决定系数也可以认为是自变量解释了因变量总变异的百分比。本例中年龄解释了尿肌酐含量79%的总变异。调整后的决定系数（

）加上了对变量个数的“惩罚”，在多重线性回归中才有意义。其计算公式为

其中，R2为决定系数，n为样本量，k为变量的个数。这里样本量为18个，变量的个数为1个，所以有：

Radj-1-(1-SSW/SST)*((18-1)/(18-2));Radj[1]0.7790901

这是命令summary(mod)显示的调整后的决定系数。

用age的均方（自由度为1）除以残差的均方可以得到F统计量的值。

(residuals(mod)^2)/mod$/;Fvalue[1]60.95444

使用F值以及它所对应的两个自由度（变量age的自由度1和残差自由度16），就可以计算检验变量age效应的p值了。

pf(Fvalue,df1=1,df2=16,=FALSE)[1]7.597353e-07

函数pf()从给定的F值与两个对应的自由度中计算p值，此结果与用命令summary(aov(mod))得到的输出结果是一致的。函数中的最后一个参数设为FALSE是为了得到曲线下方F值右侧的面积。

回归分析和方差分析给出了相同的结论，即年龄与尿肌酐含量之间有显著的线性关系。

6.1.3回归诊断

现在，我们可以在图6-1上添加一条回归直线了。

abline(mod)

图6-2中回归直线的截距约为1.45，斜率为0.15。拟合值（期望值）是指对于给定的年龄值，回归直线上对应的尿肌酐含量。残差值是观察值与期望值之间的差异，残差值可以用下面的命令画出：

points(UCR$age,fitted(mod),pch=18,col="blue")segments(UCR$age,UCR$ucr,UCR$age,fitted(mod),col="green")

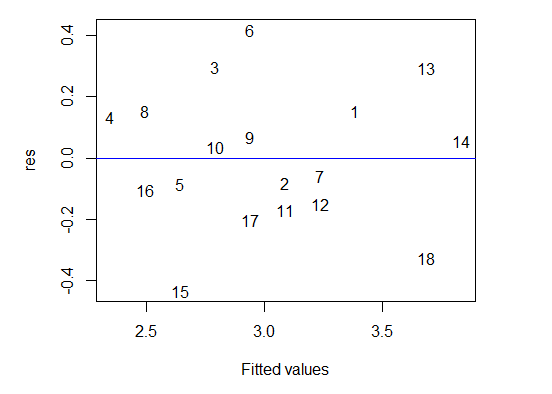
图6-2年龄与尿肌酐含量散点图及回归直线

也可以用函数residuls()从模型中提取每个样本点的残差值：

res-residuals(mod);

残差值有些是正数，有些是负数，表明在散点图中有些点位于拟合的直线上方，有些位于直线下方。其中第15个记录的残差绝对值最大，其对应的点距拟合的直线最远。我们还可以检查残差的和及其平方和：

sum(res)[1]-1.387779e-17sum(res^2)[1]0.8385279

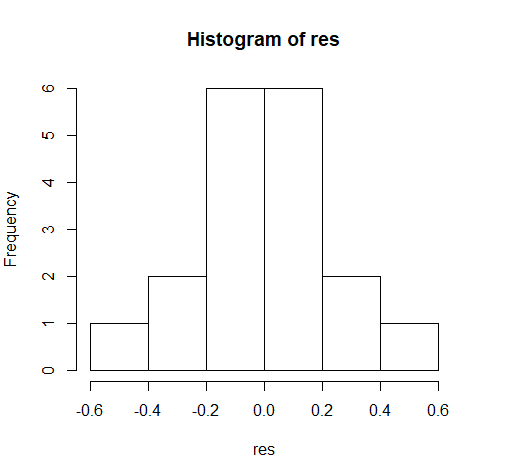
残差的和几乎等于0；残差的平方和与之前计算的结果相同。如果模型拟合得好，则残差的分布应该是正态分布。检验残差正态性的一种常规方法是查看其直方图（如图6-3所示）。

hist(res)

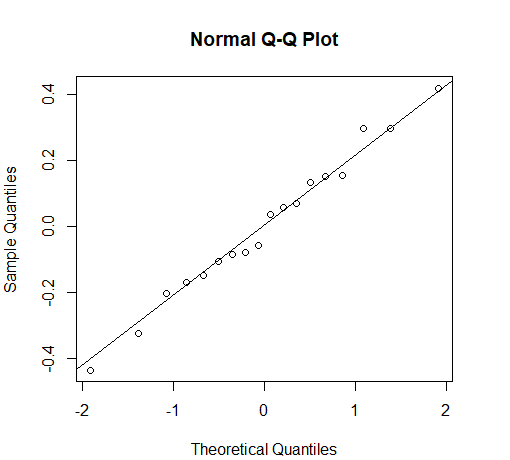
从图6-3可以看出，残差基本上呈正态分布。然而，对于这样一个小样本而言，检查正态性的一个更好的方法是作期望的标准正态分值与残差的散点图（如图6-4所示），这种图被称为正态QQ图。如果正态QQ图中的散点聚集在一条直线上，就表明残差呈正态分布。

qqnorm(res)qqline(res)

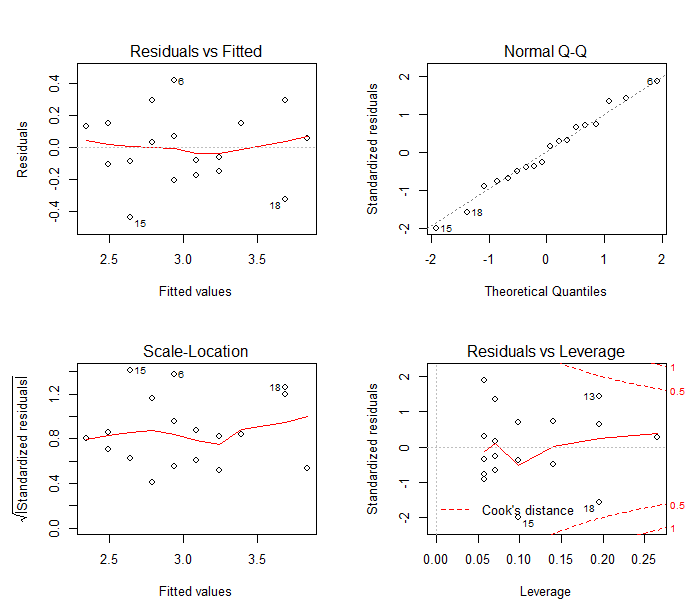
图6-3残差分布的直方图

图6-4残差分布的正态QQ图

从图6-4可以看出，散点基本上在一条直线上。定量地，可以使用Shapiro-Wilk检验。

(res)Shapiro-Wilknormalitytestdata:resW=0.98546,p-value=0.9888

Shapiro-Wilk检验的零假设是给定的数据服从正态分布。上面的p值为0.9888，可认为残差呈正态分布。

最后，我们可以作残差与拟合值之间的散点图来看残差的分布模式，绘图结果如图6-5所示。

plot(fitted(mod),res,xlab="Fittedvalues",type="n")text(fitted(mod),res,labels=rownames(UCR))abline(h=0,col="blue")

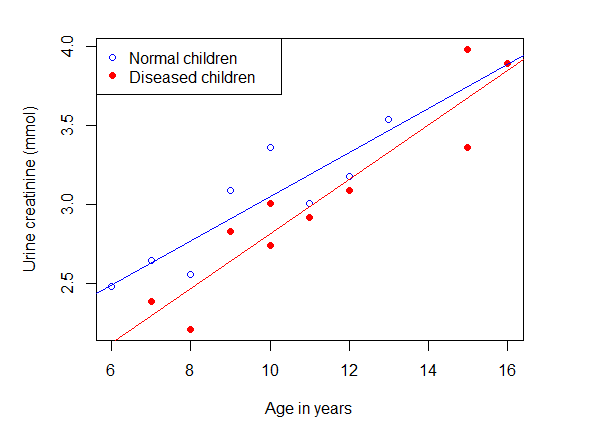
图6-5残差与拟合值的散点图

在上面的命令里，我们先在函数plot()里设置参数type为“n”（代表不显示散点），然后用函数text()在散点位置标注了样本点的编号，最后添加了一条蓝色的水平线作为参考线。从图6-5中看不出明显的模式，可认为残差独立于拟合值（期望值）。综上所述，我们可以得出残差是随机的和服从正态分布的结论。

实际上，关于模型的残差诊断图也可以通过下面的命令获得：

par(mfrow=c(2,2))plot(mod)par(mfrow=c(1,1))

因为命令plot(mod)的输出包含4幅图形，所以我们先用函数par()把画布分隔成了两行两列，作图之后又把画布恢复成默认的一行一列。图6-6不仅给出了之前绘制的两幅残差诊断图，还给出了位置尺度图（左下）和残差-杠杆图（右下）。位置尺度图主要用于检验残差的方差齐性，而残差-杠杆图主要用于鉴别离群点、高杠杆值点和强影响点。图6-6表明模型拟合效果比较理想，满足了线性模型的假设条件。

通过上述分析，我们可以得出尿肌酐含量与儿童的年龄有关联的结论。年龄每增长一岁，尿肌酐含量平均增加0.14869mmol。除去年龄这个因素，影响尿肌酐含量的其他因素可能是随机误差或是其他未考虑到的影响因素。

图6-6残差诊断图

6.2分层线性回归

通常一个数据集里包含研究中收集到的多个变量。探索两个变量在第三个分类变量的不同类别之间的关系是很有意义的，这本质上是对回归方程进行比较的问题。这里首先要检验两条（或多条）回归直线是否平行；若平行，再检验其截距是否相等。在6.1节的分析中我们把所有儿童看作一个整体，并没有考虑儿童是否患病。实际上，在数据集里还有一个因子型变量group，用于区分正常儿童和大骨节病患病儿童。

在6.1节我们已经建立一个简单线性回归模型mod，拟合了一条回归直线。模型的结果表明儿童的年龄对尿肌酐含量有显著影响。接下来探索不同类型儿童的年龄对尿肌酐含量的影响是否有显著差异。

如果假定年龄对正常儿童和患病儿童尿肌酐含量的影响是一致的，那么可以通过在模型里加入变量group拟合两条平行的回归直线。

mod1-lm(ucr~age+group,data=UCR)summary(mod1)Call:lm(formula=ucr~age+group,data=UCR)Residuals::(|t|)(Intercept)1.448930.184277.8631.06e-06*******---:0‘***’0.001‘**’0.01‘*’0.05‘.’0.1‘’1Residualstandarderror:0.2037on15degreesoffreedomMultipleR-squared:0.8457,AdjustedR-squared:0.8252F-statistic:41.12on2and15DF,p-value:8.162e-07

平均来说，年龄每增长1岁，尿肌酐含量显著增加0.16156mmol（）；在相同的年龄，患病儿童的尿肌酐含量比正常儿童平均低0.23256mmol（p=0.0373）。

下面绘制两条平行的回归直线。先作散点图，用蓝色的空心圆圈代表正常（未患病）儿童，用红色的实心圆点代表患病儿童。

col-ifelse(UCR$group==0,"blue","red")pch-ifelse(UCR$group==0,1,19)plot(ucr~age,data=UCR,+xlab="Ageinyears",ylab="Urinecreatinine(mmol)",+col=col,pch=pch)leg("topleft",+leg=c("Normalchildren","Diseasedchildren"),+col=c("blue","red"),pch=c(1,19))

然后，用函数abline()分别对每一组绘制一条回归直线。函数abline()中的参数a为截距，参数b为斜率，它们都可以由模型的系数得出。函数coef()可以用来提取模型mod1包含的系数：

coef(mod1)(Intercept)

对于两个组来说，其斜率是固定的：

b-coef(mod1)[2];

对于未患病组，变量group取值为0，其截距是系数的第一项，记为a0：

a0-coef(mod1)[1];a0(Intercept)1.448927

对于患病组，变量group取值为1，其截距为系数的第一项与第三个项之和，记为a1，其值为：

a1-coef(mod1)[1]+coef(mod1)[3];a1(Intercept)1.216368

与上面已经绘制完成的散点图一致，我们用蓝色代表未患病组、红色代表患病组，分别绘制两条回归直线，如图6-7所示。

abline(a=a0,b=b,col="blue")abline(a=a1,b=b,col="red")

图6-7两组回归直线截距的比较

在上面的模型里，我们假定儿童年龄对尿肌酐含量具有恒定的效应。然而这一假设是否成立，需要进行统计学检验。我们可以尝试用不同的斜率来拟合回归直线，然后比较两个斜率的差异是否显著。这时，需要建立一个含有变量age与group之间交互项的模型。

mod2-lm(ucr~age+group+age:group,data=UCR)

在模型的公式里，“age+group+age:group”可以简写为“age*group”。模型mod2中有4个系数：

coef(mod2)(Intercept)agegroup1age:

所以，mod2可以简化表示为：ucr=1.662+0.139×age–0.566×group+0.033×age×group。

常数项1.662是未患病组（因为age和group取值都为0）拟合直线的截距。对于患病组的截距，公式中右边的第2项和第4项均为0（因为age取值为0），但是第3项应该保留（因为group取值为1）。该项的系数为负数，表明患病组的截距比未患病组的截距小。用a0和a1分别表示未患病组和患病组的截距，则有：

a0-coef(mod2)[1];a0(Intercept)1.661667a1-coef(mod2)[1]+coef(mod2)[3];a1(Intercept)1.095732

未患病组的斜率就是第2个系数，因为group取值为0。而患病组的斜率为第2个系数和第4个系数之和，因为此时group取值为1。用b0和b1分别表示未患病组和患病组的斜率，则有：

b0-coef(mod2)[2];(mod2)[2]+coef(mod2)[4];

我们可以用这些系数绘制两条回归直线，如图6-8所示，过程与前面类似，代码如下：

col-ifelse(UCR$group==0,"blue","red")pch-ifelse(UCR$group==0,1,19)plot(ucr~age,data=UCR,+xlab="Ageinyears",ylab="Urinecreatinine(mmol)",+pch=pch,col=col)leg("topleft",+leg=c("Normalchildren","Diseasedchildren"),+col=c("blue","red"),pch=c(1,19))abline(a=a0,b=b0,col="blue")abline(a=a1,b=b1,col="red")

图6-8两组回归直线斜率的比较

图6-8显示两条回归直线不平行（斜率不相等），表示年龄在两组中的效应不一致。这种不一致可能是由偶然因素（随机误差）所导致的，也可能是由是否患病所导致的。下面用函数summary()查看各个回归系数有无统计学意义。

summary(mod2)Call:lm(formula=ucr~age*group,data=UCR)Residuals::(|t|)(Intercept)1.661670.309825.3630.000100******::0‘***’0.001‘**’0.01‘*’0.05‘.’0.1‘’1Residualstandarderror:0.2055on14degreesoffreedomMultipleR-squared:0.8535,AdjustedR-squared:0.8221F-statistic:27.18on3and14DF,p-value:4.257e-06

交互作用项“age:group1”的系数没有统计学意义（p=0.405152），即这两个斜率的不同是偶然因素所导致的。所以，在模型中没有必要包含这个交互项，mod1就是最终的模型。

6.3多重线性回归

现实世界中事物之间的关系是错综复杂的，一个变量的变化往往与另外很多个变量的变化有关。比如人的心率与年龄、体重、肺活量等有关。在线性回归中，如果解释变量的个数多于一个，这种模型称为多重线性回归模型。

多重线性回归模型假定因变量Y受多个自变量

的影响，并且因变量与这些自变量之间存在线性关系，模型可表示为

其中，

被称为常数项，

被称为偏回归系数；随机误差ε服从均值为0、方差为σ2的正态分布。对于这些参数，通常由样本观测值利用最小二乘法估计得到。

6.3.1拟合多重线性回归模型

下面以ISwR包里的数据集cystfibr为例介绍多重线性回归。该数据集来自一项关于囊胞性纤维症患者肺功能的研究。先安装并加载ISwR包，然后查看数据集cystfibr里的变量。

library(ISwR)data(cystfibr)?cystfibrstr(cystfibr)'':25:$age:int77888911121213$sex:int0101001101$height:int1091121241251276155$weight:$bmp:int68656467936889696768$fev1:int321922423$rv:int258449441234202308305369312413$frc:int68194225$tlc:int41041136$pemax:int9585100859580651107095

根据数据集cystfibr帮助文档中的说明，变量sex表示性别，其中0代表男性，1代表女性，这里需要把它转换成因子。

cystfibr$sex-factor(cystfibr$sex,labels=c("male","female"))

数据集里最后5个变量分别为fev1（第一秒用力呼气量）、rv（残气量）、frc（功能残气量）、tlc（肺总气量）和pemax（最大呼气压）。这些变量都是测量肺功能的指标，我们可以用函数cor()查看它们之间的相关性。

cor(cystfibr[,6:10])

从相关系数矩阵可以看出，这5个变量之间有较强的相关性。为了简化问题，下面选用其中的变量fev1作为结果变量建立多重线性回归模型。

fit1-lm(fev1~age+sex+height+weight+bmp,data=cystfibr)summary(fit1)Call:lm(formula=fev1~age+sex+height+weight+bmp,data=cystfibr)Residuals::(|t|)(Intercept)19.2879443.463840.4440.6622*:0‘***’0.001‘**’0.01‘*’0.05‘.’0.1‘’1Residualstandarderror:8.788on19degreesoffreedomMultipleR-squared:0.5123,AdjustedR-squared:0.384F-statistic:3.992on5and19DF,p-value:0.01209

与简单线性回归类似，多重线性回归也是用最小二乘法拟合模型。模型的输出结果也与简单线性回归相似，此处不再赘述。注意到变量sex后面加了“female”，这是因为R以哑变量的形式处理分类变量（因子），未被显示的水平（这里是“male”）作为参考组。结果显示，仅变量sex（性别）对应的t检验有统计学意义，女性患者的fev1值平均比男性患者低约10个单位，其余变量均无统计学意义。而对模型的方差分析（F检验）是显著的（p=0.01209）。决定系数为0.5123，表明fev1变异的51%可由上述5个自变量的变化来解释。