摘要:基于高速公路的历史联网收费数据,以行程时间为预测对象,对高速公路行程时间预测模型的适用性进行了探讨研究。研究选取了福建省的南北中3个实验路段进行同步对比,提取行程时间及进站流量的时间序列,挖掘交通流特征变量并分析相关性,构建模型输入矩阵,同时用相同数据集对行程时间进行多模型预测和结果对比,结果表明LSTM模型基本可以反映行程时间的变化趋势,且预测精度高于传统的MA、ARIMA,以及ANN、RNN等神经网络模型,可实现对行程时间的有效预测。同时,3段实验路段的路网功能、交通组成、区位特征均有所不同,初步验证了模型预测用于不同类型高速公路的可行性,可为此方面研究应用提供一定参考。
关键词:交通调查;行程时间预测;收费数据;长短时记忆网络;误差分析;
高速公路联网收费数据信息量大,随着技术手段和预测模型的不断发展,挖掘数据的潜在价值,进行高速公路交通运行状态的特征分析,使得历史联网收费数据为管理者提供管理辅助成为可能。相对于检测设备和手机信令的信息获取手段,联网收费数据具有以下特点:联网收费系统随高速公路建成即投入使用,历史收费数据库已经存在,数据质量稳定,信息格式统一,因此具备可靠、经济和便利等优点。可见,各类数据在数据获取和质量上各有所长,利用高速公路联网收费数据可以在现有设备和已有信息的基础上直接进行研究,是一种经济高效的手段,可与其他类数据的研究应用互为补充,在高速公路信息化管理中发挥作用。
传统的交通流预测模型包括参数化模型和非参数化模型。基于统计理论的参数化模型主要包括线性回归、自回归滑动模型ARMA、卡尔曼滤波等方法,该类模型以平稳假设为前提,参数较少,模型相对简单。Kwon等利用高速公路流量、占用率的数据建立线性回归模型,对行程时间进行了预测[9];杨连成等融合高速公路收费和气象数据对行程时间进行预测,引入回归变量的ARMAX模型较ARMA预测精度有所提升[10]。非参数化模型包括各类神经网络、支持向量机等。这类模型往往可以捕捉交通等多元数据中深层次的特征,与参数化模型相比预测精度较高,但同时模型结构更为复杂。郎妍建立了基于BP神经网络和梯度校正法的行程时间预测模型,对城市环路的交通拥堵状况进行分析[11];邢雪等以交通数据实际特征作为行程时间历史数据集分类的依据,基于强度修正的K-means方法较自回归模型提高了预测的准确性[12]。基于RNN神经网络演化的长短时记忆神经网络模型LSTM(LongShort-TermMemory)通过增加细胞状态和门控机制将长时间的信息保留,可以解决长序列训练过程中的梯度消失和梯度爆炸问题。张威威等利用LSTM模型预测城市道路出行时间,与传统BP神经网络等4种模型对比,考虑空间相关性的LSTM模型具有更好的拟合效果[13]。
LSTM模型克服了长期依赖的问题,对长时间序列较强的学习能力,使其在预测中有更好的表现,高速公路行程时间预测也是一个典型的长时间序列问题,因此本文选取福建省的南北中三段高速公路进行同步对比,对LSTM模型在高速公路行程时间预测上适用与否进行研究。首先,提取行程时间及流量的时间序列,挖掘交通流特征变量并分析相关性,在此基础上构建LSTM的输入矩阵;同时,用相同数据集进行多模型预测对比,用误差计算结果来评判预测效果。
本文使用的原始数据取自福建省高速公路联网收费数据,分别从福建省南部、北部和中部,选取了其中3段有代表性的高速公路。路段一:G15沈海高速漳浦至古雷港段,起讫点收费站分别为漳浦收费站、古雷港收费站,路段长15km,上下高速公路的日单向流量可达2200辆以上。路段二:G1514宁上高速福安至赛岐段,路段长12.6km,驶入福安收费站且从赛岐收费站驶出的日单向流量可达2200辆以上。路段一、二均属国高网。路段三:S81福州东快安至福州机场段为机场高速公路,属福建省高网,路段长25km,驶入福州东快安收费站且从福州机场收费站驶出的日单向流量可达4500辆以上。
高速公路节假日和工作日的交通流特征明显不同,本次研究选择上述3段高速公路某年12月9日、12月23日两个工作日的全天收费数据,以12月9日数据作训练集、12月23日数据作测试集。
车辆在起点收费站和终点收费站的收费信息,形成该车上下高速公路的一条收费记录,每条收费记录的数据字段如表1所示,包括记录日期、车牌号码、进口收费站ID、进站时间、出口收费站ID、出站时间等内容。本文所指的行程时间即为某车收费信息中出站时间与进站时间的差值。路段一、二、三的原始收费记录,12月9日分别为2188条、2538条、4539条,12月23日分别为2364条、2616条、4678条。
表1收费记录的数据字段含义导出到EXCEL
字段
类型
含义
示例
date
datetime
记录日期
20**12
car_id
int64
车牌号码
蓝闽A9****
o_id
int64
进口收费站ID
3304
o_time
datetime
进站时间
10.12.14
d_id
float64
出口收费站ID
3104
d_time
datetime
出站时间
10.32.01
class
int64
车辆类型
1
对上述路段原始收费记录进行数据清洗,去掉错误、异常数据,保留有效样本,在数据可靠和有效性上满足模型分析处理的需要。其中,时间显示异常、记录不完整和缺失的直接剔除,通过筛选去除行程时间明显偏离合理区间的数据。以下为路段三12月9日当天数据清洗示例。
进站时间、出站时间不在统计时间范围内的记录98条,如进站时间显示为“1900-01-01”;进出站时间完全一致或出站时间早于进站时间的记录46条。
数据中存在某些字段缺失的有204条,如进站ID显示为“0”、进站时间为汉字、重复记录等。
研究中通过设置合理时间区间进行筛选,对行程时间超出区间的收费记录予以剔除,此类共46条。合理时间区间设置方法如下。
采用高速公路限速与四分位法相结合的方法,将起讫点收费站之间的里程与限速的比值作为行程时间的最小值,将四分位法的上截断点作为行程时间最大值,计算公示如下:
Tmin=L/Vmax(1)
Tmax=T75%+1.5×(T75%-T25%)(2)
式中:L为高速公路长度;T25%为行程时间的25%分位数;T75%为行程时间的75%分位数;Tmin为行程时间的最小值;Tmax为行程时间的最大值。
数据清洗前后对比结果如图1,图2所示,对比可以看到通过数据预处理,数据集去除了错误异常的个例,保留了大部分可以表现行程时间变化趋势的数据。
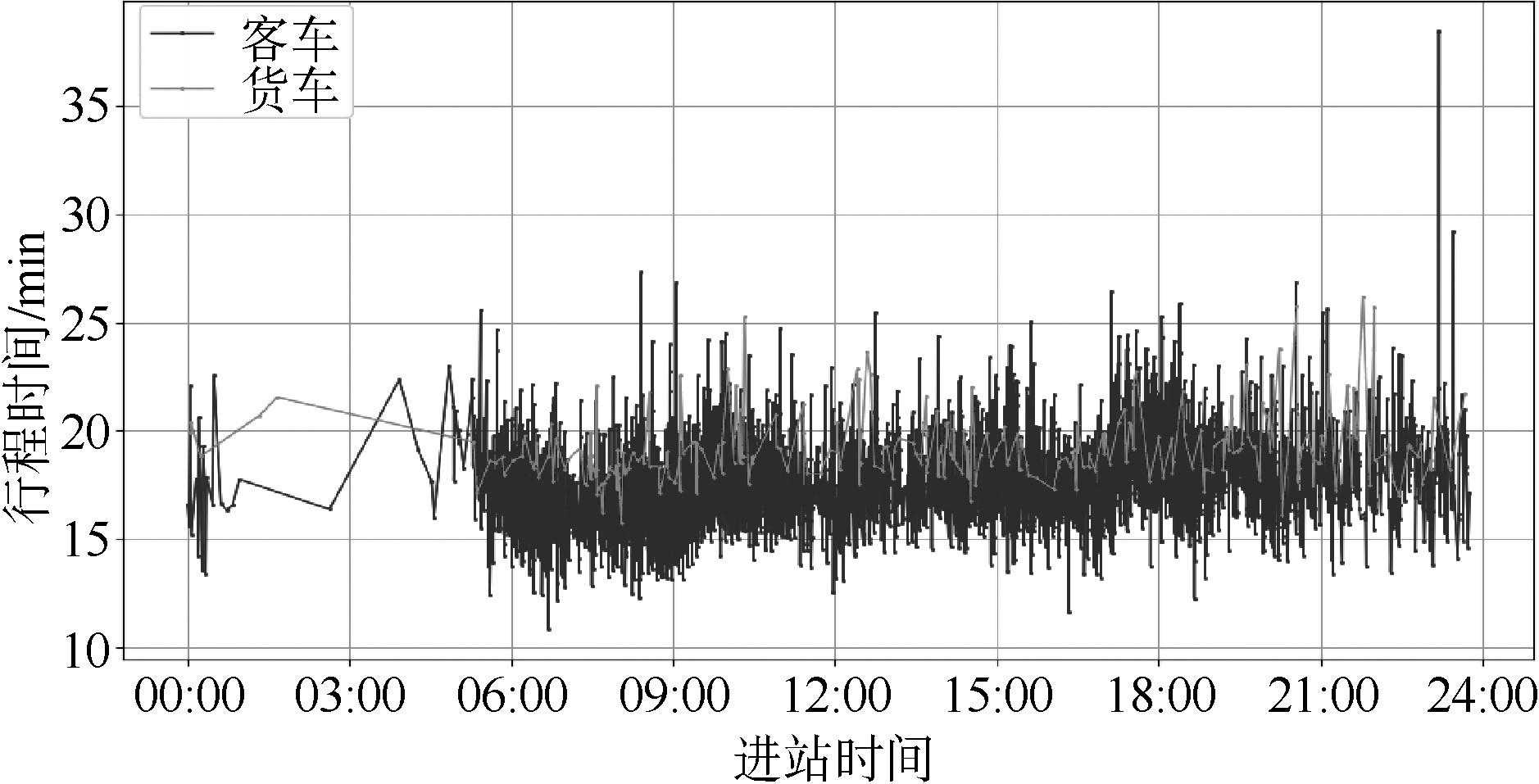
图1路段三行程时间分布(清洗前)下载原图
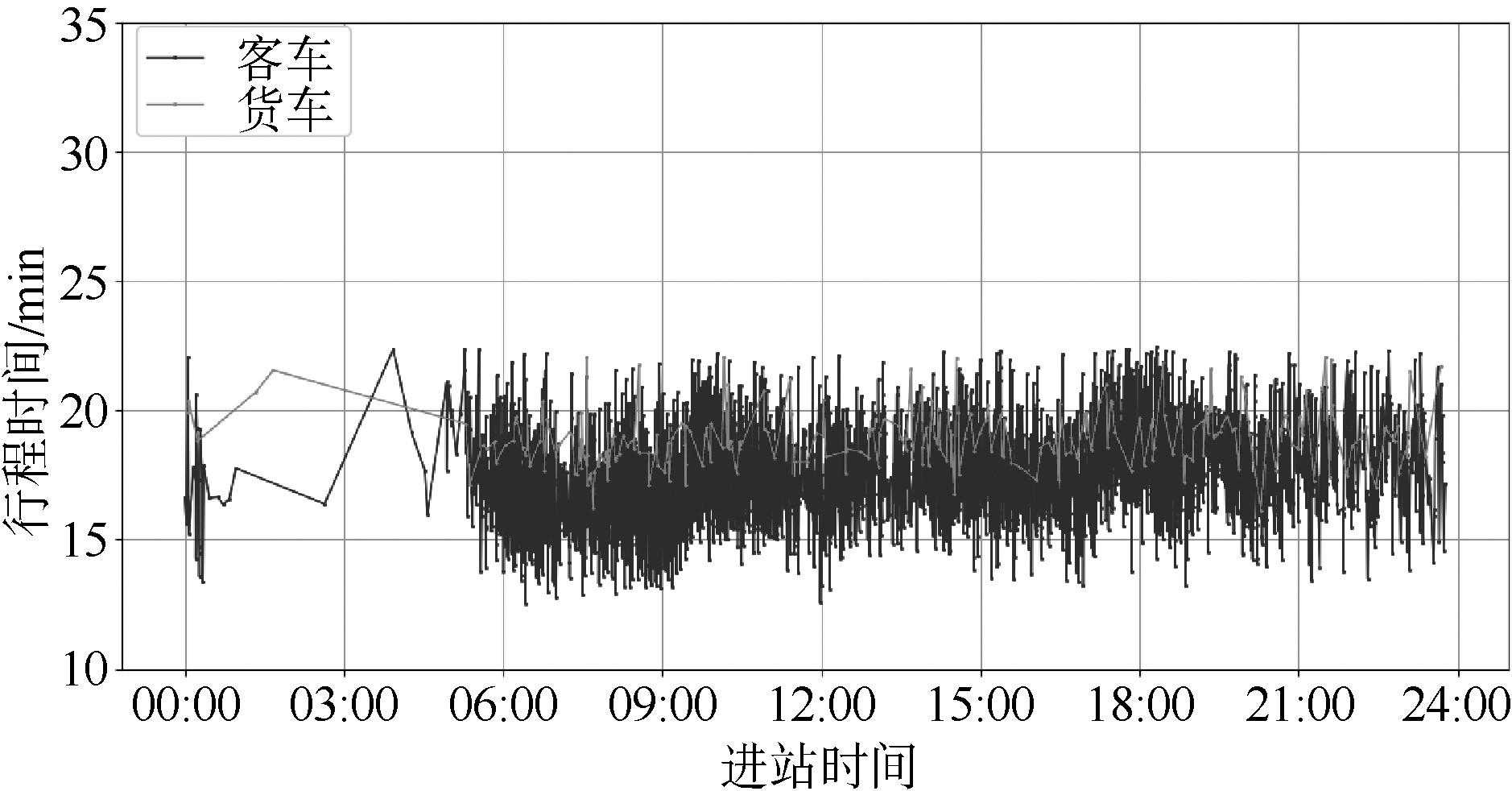
图2路段三行程时间分布(清洗后)下载原图
经过数据清洗,3个路段原始样本与有效样本数量对比如表2。
表2原始样本与有效样本数量对比导出到EXCEL
日期
路段
原始样本数量
剔除数量
有效样本数量
进出站时间
字段
行程时间
12月9日
路段一
2188
61
86
15
2026
路段二
2538
35
104
23
2376
路段三
4539
144
204
64
4127
12月23日
路段一
2364
79
26
9
2250
路段二
2616
68
34
53
2461
路段三
4678
114
168
32
4364
本研究提出了基于收费数据的高速公路行程时间预测方法的整体框架,如图3所示,主要包括数据预处理模块、模型训练模块和模型校验模块等3个部分。
第一步数据预处理模块,首先选择合适的时间间隔,将多条收费记录数据转化为流量、行程时间的时间序列,然后分析挖掘高速公路交通流的变量特征和之间的相关性,并以此构建模型的输入矩阵。
第二步模型训练模块,根据输入矩阵建立输入层、隐藏层、输出层,基于LSTM模型对训练集数据进行多轮迭代,以均方误差为损失函数,在优化器的作用下对模型各参数进行寻优。
第三步模型校验模块,利用测试集数据在训练后对LSTM模型进行校验,同时采用其他模型做测试对比,通过误差计算来判断预测方法的可行性和LSTM模型的适用性。
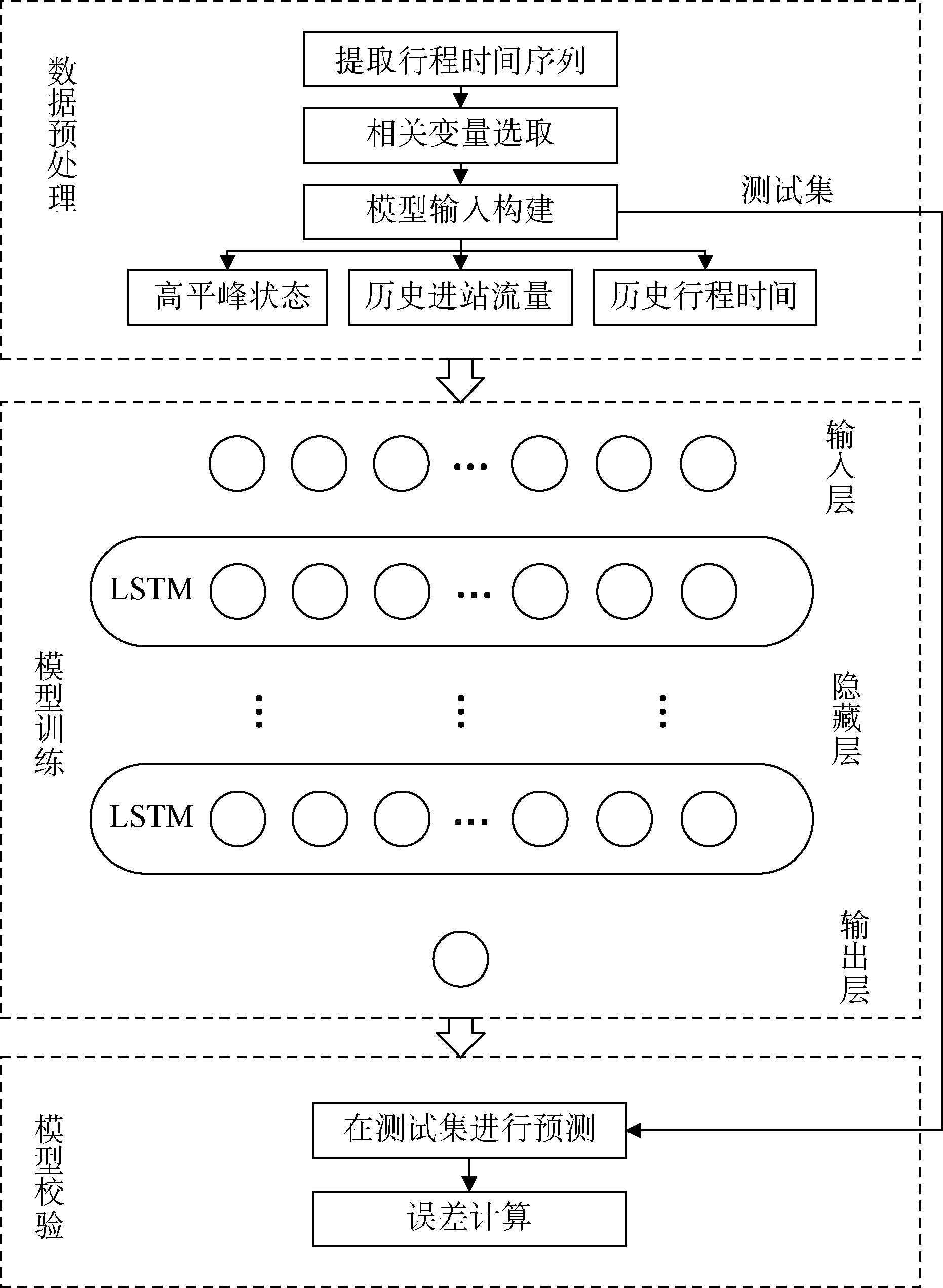
图3基于收费数据的高速公路行程时间预测方法框架下载原图
LSTM的门控机制包括遗忘门(ForgetGate)、输入门(InputGate)和输出门(OutputGate),门控机制可有效决定每一次输入信息的传递与保存。将第t个时间间隔的遗忘门定义为ft,输入门定义为it,输出门定义为ot,细胞状态定义为Ct。首先输入的信息通过遗忘门来决定哪些部分需要被遗忘,输入xt和前一时间间隔的输出ht-1通过输入门进入到细胞状态,结合前一时间间隔的细胞状态Ct-1更新Ct,最后通过输出门决定哪些信息可以输出。公式如下
ft=σ(Wxfxt+Whfht-1+bf)(3)
it=σ(Wxixt+Whiht-1+bi)(4)
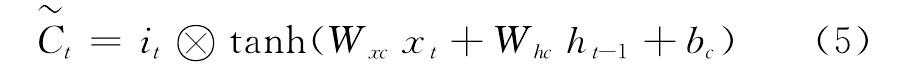
ot=σ(Wxoxt+Whoht-1+bo)(6)
ht=ot⨂tanh(Ct)(7)
式中:W和b为3个门控机制对应的权重矩阵和偏置;σ代表sigmoid函数;tanh代表双曲正切激活函数。LSTM的神经元结构如图5所示。
以预测值与实际值的均方误差最小化为目标,在Adam优化器的作用下,对模型网络各参数不断进行更新,模型的预测结果不断优化。

图4LSTM神经元结构下载原图
为了将单条收费数据记录转换为时间序列,需要确定时间间隔的合理长度。本文以10min、15min、20min、30min为时间间隔分别进行统计,以路段三为例,结果如图5所示。对比其他各时间间隔,20min既保留了行程时间的变化趋势,又消除了部分随机波动,可满足预测需求,因此本文以20min作为时间间隔的基本单位来构造各相关的时间序列。
根据实际情况,在凌晨0:00至6:00期间流量小,行驶速度接近于自由流,故研究将预测时间段定义为6:00~24:00之间,以20min为单位将6:00至24:00划分为54个时间间隔。至此收费记录整合后,形成进站流量和行程时间的时间序列。时间序列的序号t:0~53,分别对应具体时间间隔:6:00~6:20、6:20~6:40、6:40~7:00,…,23:40~24:00;进站流量Ct:第t个20min间隔内驶入起点收费站的车辆合计数;行程时间Tt:第t个20min间隔内对应车辆的行程时间算术平均值。
本文从进站流量的时间分布规律、行程时间趋势变化特征入手,提取建模变量,对相关性进行量化分析。
本次原始数据中货车占比少,加之货车司机对时间成本相对不敏感,因此以下预测分析主要以客车为研究对象。3段高速公路的进站流量24h分布如图6所示,可以看出,进站流量全天内呈现明显的分布特征,均在上午或下午出现高峰或次高峰,按照高峰、次高峰和平峰3个特征将6:00~24:00进行划分(见表3),以此为基础为相应时段内的数据进行标签分类。
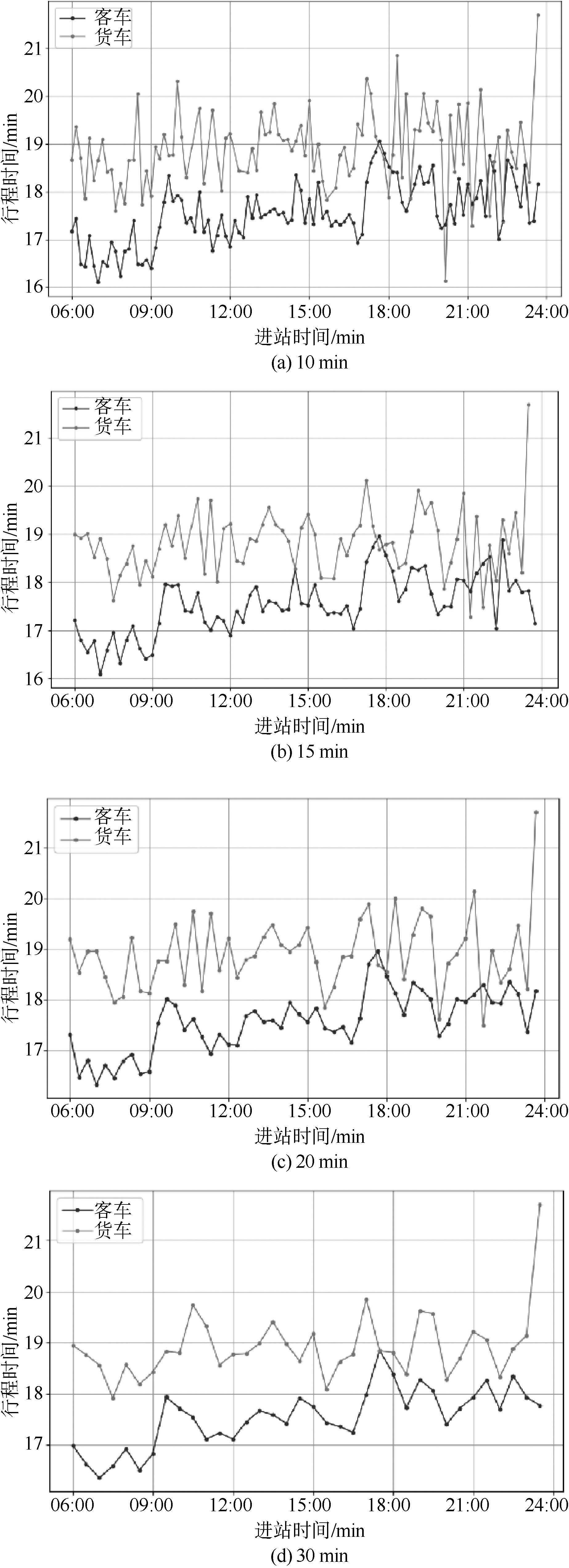
图5不同时间间隔下行程时间分布下载原图
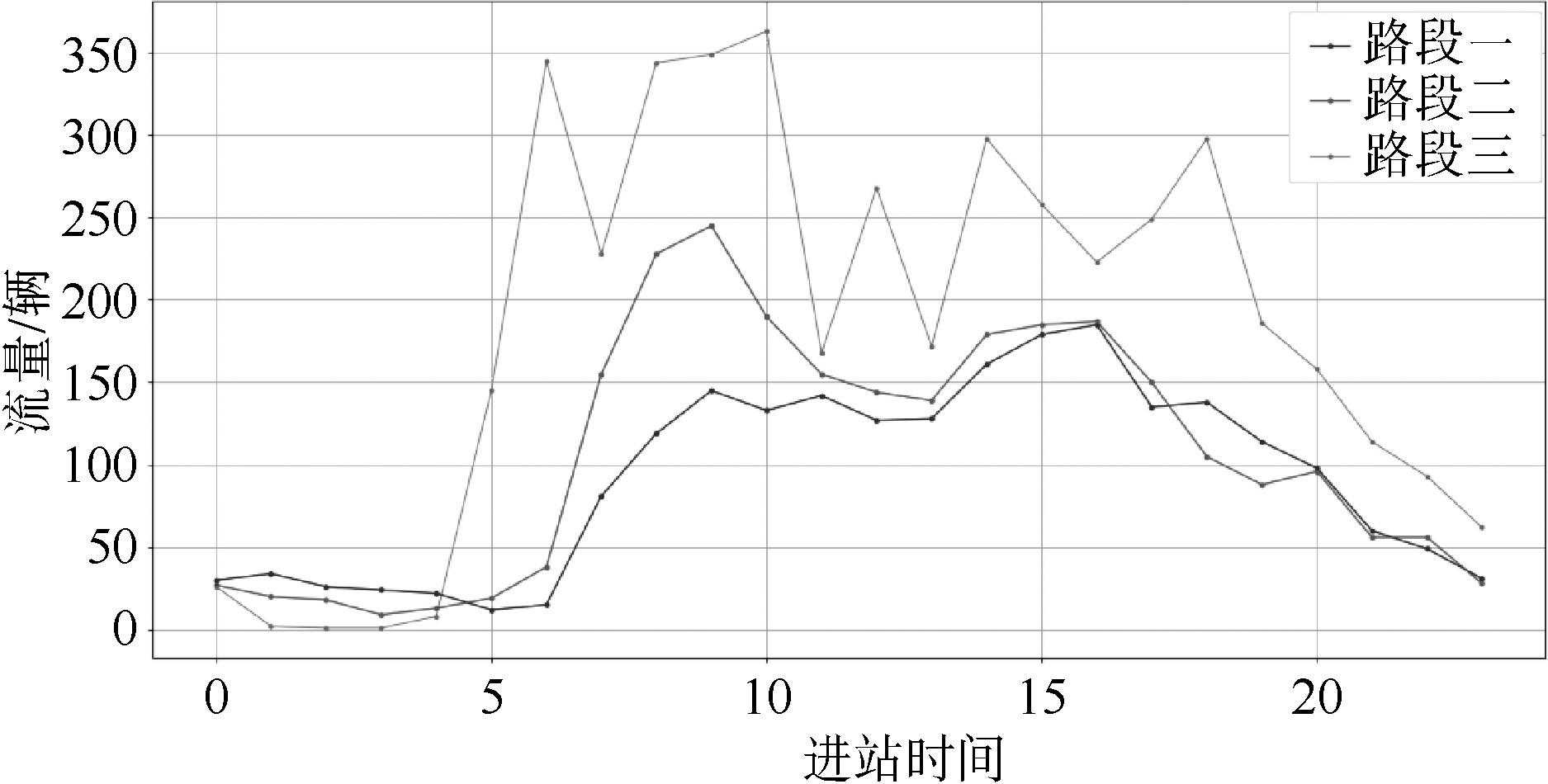
图624h进站流量分布下载原图
表3高平峰状态分布导出到EXCEL
状态分类
路段一
路段二
路段三
高峰
8:00~10:00
14:00~17:00
6:00~7:00;
8:00~11:00
次高峰
7:00~8:00;
10:00~18:00
9:00~14:00;
17:00~20:00
7:00~8:00;
11:00~20:00
平峰
6:00~7:00;
18:00~24:00
6:00~9:00;
20:00~24:00
20:00~24:00
通常情况下相邻时间间隔内的行程时间相近,且因实际道路拥堵状况,行程时间与进站流量呈现一定的趋势和规律。本文针对前续10个时间间隔,对行程时间趋势变化、行程时间与进站流量的相关性进行分析。
图7可以看出,3段高速公路的行程时间Tt与前序行程时间Tt-i均呈正相关,路段二相关系数波动较大,路段一、三波动相对平稳,3个路段与Tt相关系数最大的均为临近的Tt-1、Tt-2;而行程时间Tt与进站流量Ct-i相关性结果显示,路段二、三为负相关,路段一则呈正相关,3个路段的相关系数波动均不大,但是与行程时间Tt相关系数最大的流量在时间上都呈现一定的延后性,如路段一Tt与进站流量Ct-5和Ct-6正相关最大,而路段二、三分别与Ct-1和Ct-2、Ct-2和Ct-3的负相关最大。
以前述提取的行程时间与相关变量,对模型输入进行构建。高平峰状态St为分类变量,以哑变量方式编码,St=0代表高峰,St=1代表次高峰,St=2代表平峰。对3段高速的输入数据进行归一化处理,去除量纲对预测结果的影响后,将输入数据切分训练集与预测集,构建输入矩阵XT和YT。以路段三为例,公式如下:
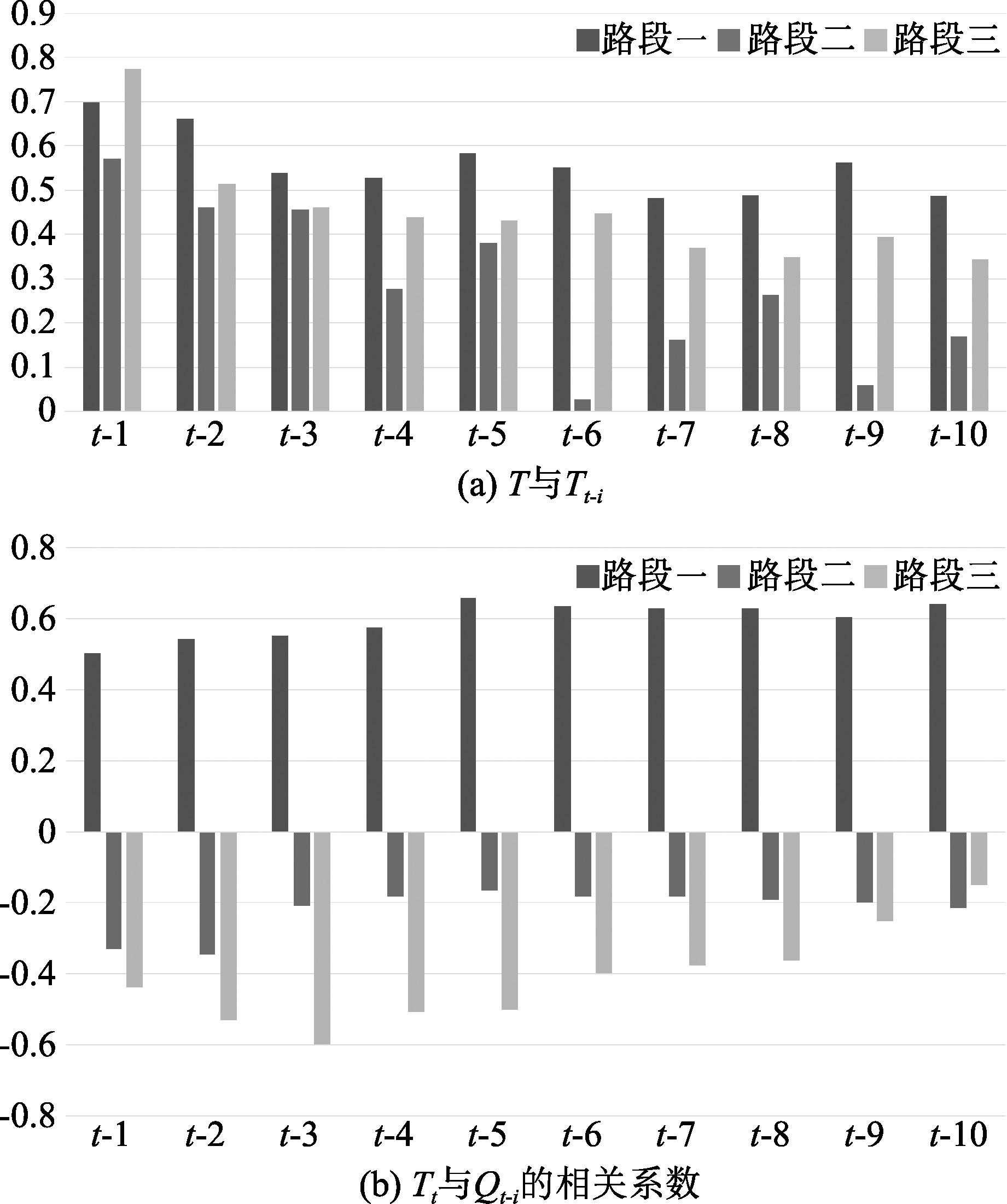
图6历史10个时间间隔的相关系数下载原图
XT=⎡⎣⎢⎢⎢⎢StSt−1⋮S3Tt−1Tt−2⋮T2Tt−2Tt−3⋮T1Ct−2Ct−3⋮C1Ct−3Ct−4⋮C0⎤⎦⎥⎥⎥⎥(8)XΤ=[StΤt-1Τt-2Ct-2Ct-3St-1Τt-2Τt-3Ct-3Ct-4⋮⋮⋮⋮⋮S3Τ2Τ1C1C0](8)
YT=[TtTt−1⋯T3](9)YΤ=[ΤtΤt-1⋯Τ3](9)
预测实验选取均方误差(MeanSquaredError,MSE)和平均绝对百分比误差(MeanAbsolutePercentageError,MAPE)为评价指标。
以12月9日收费数据作为训练集,以12月23日收费数据作为测试集。3段高速公路的行程时间预测值与实际值的对比如图7所示。
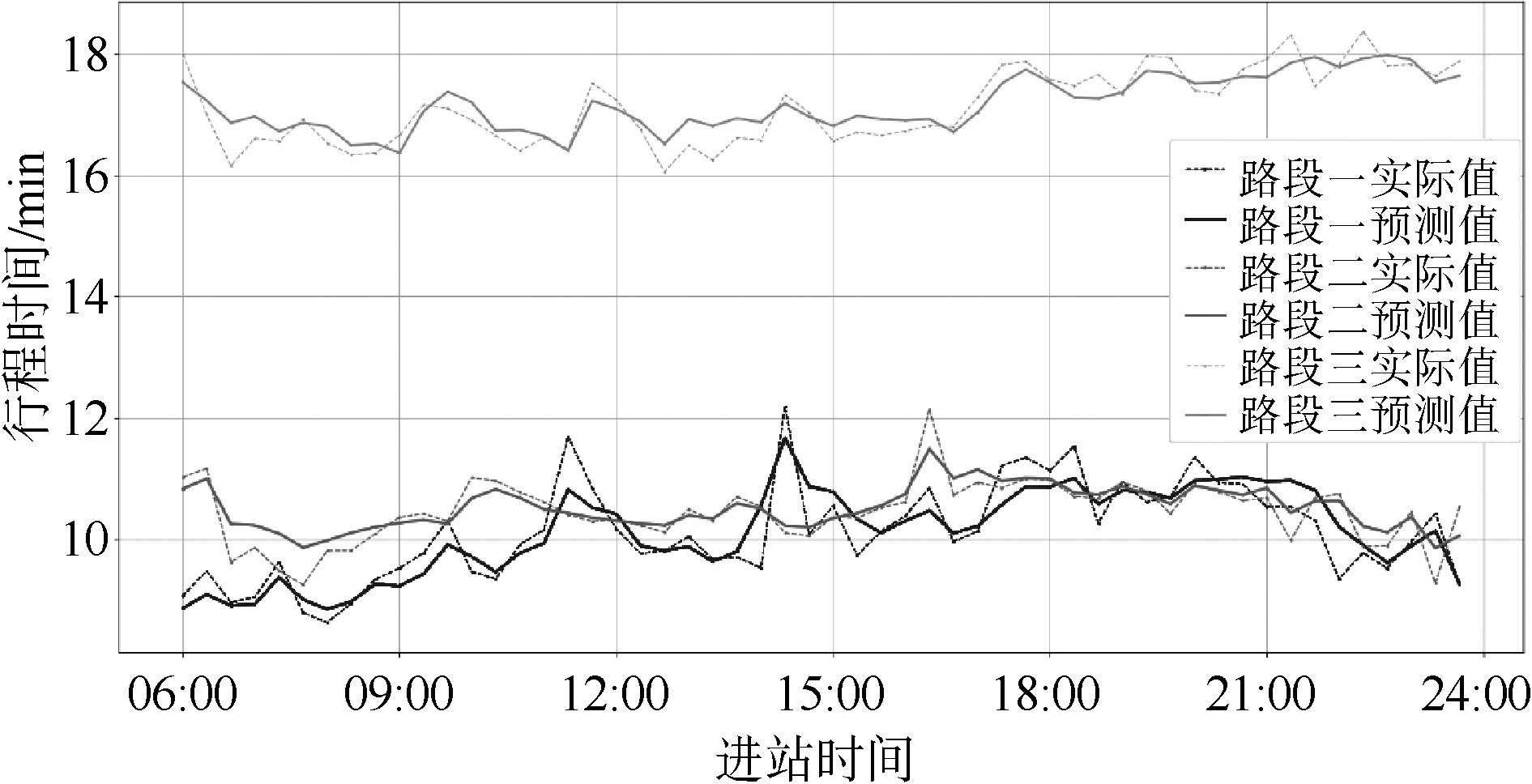
图7预测值与实际值对比下载原图
总体来看,预测值基本可以反映行程时间实际值的变化趋势,预测效果较好,路段二的MSE值最小为0.098,路段三的MAPE值最小为1.49%。LSTM模型可以捕捉不同类型高速公路行程时间序列历史特征,各高速公路的预测值与实际值的整体吻合度均较高。
基于相同数据集利用RNN、ANN、MA、ARIMA模型,分别对实验中的3段高速公路进行预测对比,误差结果见表4。可以看出,LSTM对比其他几个模型的均方误差和平均绝对百分比误差都较小,预测精度更高,预测结果明显优于其他模型,说明LSTM在高速公路行程时间预测方面有更好的表现,基于LSTM模型实现了对行程时间的有效预测。
表4预测结果对比导出到EXCEL
模型
路段一
路段二
路段三
MSE
MAPE
MSE
MAPE
MSE
MAPE
MA
1.092
10.56%
0.892
9.21%
0.987
8.98%
ARIMA
0.629
8.81%
0.523
6.08%
0.506
4.60%
ANN
0.439
5.98%
0.301
5.88%
0.266
2.74%
RNN
0.381
4.41%
0.278
3.51%
0.254
2.58%
LSTM
0.236
3.11%
0.098
1.90%
0.157
1.49%
本文基于福建省3段实验路段的历史收费数据,提出了高速公路行程时间预测的框架方法,通过数据预处理、模型训练、模型校验3个步骤,对LSTM模型的适用性进行了探讨。
(1)研究了不同时间间隔下行程时间分布特征,以合适的时间间隔提取到的高速公路行程时间、进站流量的时间序列,既可保留时间序列的时间变化趋势,又可消除部分随机波动。
(2)影响行程时间预测的变量特征分析显示,实验路段的进站流量全天呈现明显的分布特征,当前行程时间和邻近时间间隔的行程时间相关性较大,与进站流量均呈现一定的延后相关性。
(3)建立了基于联网收费数据的高速公路行程时间预测框架,实现了在仅有联网收费数据情况下的行程时间预测,并在3段高速公路上进行实验,验证了模型的适用性。
(4)通过对比均方误差和平均绝对百分比误差,结果显示LSTM模型预测精度较高,基本可以反映行程时间的变化趋势,且预测精度高于传统的MA、ARIMA,以及ANN、RNN等神经网络模型,基于LSTM模型可实现对时间的有效预测。
(5)对不同类型高速公路的可行性进行了初步验证,3段实验路段地处福建省内,路网功能、交通组成、区位特征均有所不同,具有一定代表性,可为福建省域内此类研究应用提供一定的基础和参考。
行程时间预测模型的结果可应用于高速公路智能交通系统中交通信息发布、道路服务水平评价、拥堵预警等方面,同时也可为交通流诱导和线路优化提供数据基础,服务于交通管理者与出行者。受限于数据时间跨度和样本量,本文利用有限时段和路段的收费数据对客车行程时间进行预测,虽未能将时间序列的特征进行全面刻画,但可作为行程时间预测研究的基础性工作。未来可增加月份、星期、节假日等属性,考虑天气、交通事件及车型差异等因素做进一步研究。
[1]姚智胜,邵春福,熊志华.支持向量机在路段行程时间预测中的应用研究[J].公路交通科技,2007,24(9):96-99.
[2]王志建,李达标,崔夏.基于LSTM神经网络的降雨天旅行时间预测研究[J].交通运输系统工程与信息,2020,20(1):137-144.
[3]吴庚.神经网络应用于高速公路交通流预测的研究[D].大连海事大学,2015.
[4]杨迪,李松江,邱宁佳等.基于卷积神经网络的高速公路交通流预测方法:中国,CN108205889A[P].2018.
[5]VanajakshiL,ime[C].2007IEEEIntelligentVehiclesSymposium:600-605.
[6]WosykaJ,—timetraveltimeestimationonhighwaysusingloopdetectordataandlicenseplaterecognition[C].2012Elektro:391-394.
[7]ShenL,rdata[J].JournalofAdvancedTransportation,2013,47(5):526-535.
[8]杨中岳.基于神经网络模型的高速公路交通运行状态预测方法[J].中国交通信息化,2021,(6):113-115+125.
[9]KwonJ,CoifmanB,orData[J].TransportationResearchRecordJournaloftheTransportationResearchBoard,2000,1717:1819-25.
[10]杨成连,文涛,李洋洋.基于ARMAX模型的高速公路行程时间预测研究[J].公路交通科技:应用技术版,2020,16(4):301-307.
[11]郎妍.基于梯度校正法的交通数据融合和行程时间预测研究[D].北京交通大学,2008.
[12]邢雪,于德新,田秀娟,程泽阳.基于数据挖掘的高速公路行程时间预测[J].华中科技大学学报:自然科学版,2016,44(8):36-40.
[13]张威威,李瑞敏,谢中教.基于深度学习的城市道路旅行时间预测[J].系统仿真学报,2017,29(10):2309-2315+2322.

版权声明:本站所有作品(图文、音视频)均由用户自行上传分享,仅供网友学习交流,不声明或保证其内容的正确性,如发现本站有涉嫌抄袭侵权/违法违规的内容。请举报,一经查实,本站将立刻删除。